
简单来说,一开始它是来源于生活的“经验”,后来被抽象成了数学规则,成了数学的运算的基石。
但我们不能这么给孩子说,给孩子讲还得从长计议。
做四则运算的时候:
有些孩子总忘记要“先乘除后加减”;
有些孩子记得老师的话,但他们很疑惑——why?
"为什么要有这个规定?谁规定的?" ……
说实话,很多家长自己也不明白"先乘除后加减"到底是怎么来的,只是知道"这是规则",但说不出背后的道理。
今天,我们来彻底弄清楚这个问题。

01
用生活场景来解释“整体”这个概念
场景1:买巧克力
小明原来有5颗巧克力,妈妈从超市买回来8盒巧克力,每盒6个。 现在小明一共有多少颗巧克力?
列算式:5 + 6×8
如果先算加法:5+6=11,然后11×8=88
现实中:妈妈买的是8盒,每盒6个,所以总共买了48个(6×8),再加上小明原来有的5个,总共是53个。
答案是53,不是88。
你看,"6×8"这里描述的是"妈妈买的巧克力总数",这是一个整体。
请注意:整体。

"5"是小明原来有的巧克力,这是另一个整体。
我们要先把"6×8"算出来,才能和"5"加在一起。
先算加法,就破坏了"整体"这个概念。
场景2:给学生分笔
班上有63个学生,老师要给每个学生发一支笔。老师手里有22块钱,每支笔2块钱。 问,花完这笔钱后,老师还差多少支笔?
列算式:63 - 22÷2
如果先算减法:63-22=41,然后41÷2=20.5
但现实中:22块钱能买多少支笔?22÷2=11支。
63个学生需要63支笔,所以还差52支。
答案是52,不是20.5。
"22÷2"描述的是"老师这笔钱能买多少支笔",这也是一个整体。
"63"是学生总数,这是另一个整体。
我们要先把"22÷2"算出来,才能从"63"里减去。
先算减法,又破坏了"整体"这个概念。
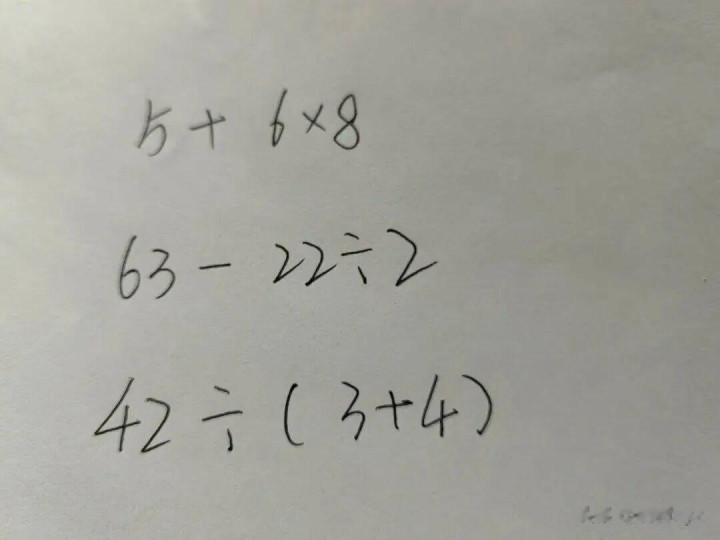
02
括号又是什么?
孩子可能会问: "那括号是干嘛的?"
括号,就是给某些运算加一个"VIP通道" 。
我们再用一个场景来解释。
场景3:分苹果
现在有42个苹果,本来有3个小朋友,后来又来了4个小朋友。 问,每个小朋友可以分到几个苹果?
列算式:42÷(3+4)
如果没有括号:42÷3+4,米兰体育官网先算42÷3=14,然后14+4=18,每个小朋友18个苹果?!
但现实中:苹果总数42个,小朋友总数3+4=7个,所以每个小朋友分到6个(42÷7)。
答案是6,不是18。
"3+4"描述的是"小朋友总数",这是一个整体。
如果没有括号,先算42÷3,就破坏了"小朋友总数"这个整体。
括号就是为了让我们先算括号里的——给这个加法运算开个vip通道。
因为它也是一个整体,不能拆开。

03
核心逻辑
乘法和除法,描述的是一个整体
6×8:8盒,每盒6个,这是一个整体
22÷2:22块钱,每支笔2块钱,这也是一个整体
加法和减法,是对整体进行组合或分割
5+6×8:小明原来的5个,加上妈妈买的6×8个
63-22÷2:63个学生,减去老师能买的22÷2个
括号,是人为地制造一个整体
3+4本来是两个数,加上括号后,它们就变成了一个整体(小朋友总数)
所以,先乘除后加减,本质上是: 先计算"整体",再对"整体"进行组合或分割。
这不是人为的规则,而是生活直觉的直接反映。
日本数学家远山启在《数学与生活1》这本书里说过:
数学是来源于生活的,基于生活中大量的实际经验、生活直觉,然后做了相应的规定。
也就是人类一开始自然使用一些的方法,后来数学家把这些"自然方法"抽象成了规则,写进了教科书。

04
谈点思维
其实"先乘除后加减"不止是四则运算中的一个规则,而是生活逻辑、数学逻辑。
它看起来很小,却是整个数学计算的基石。
再后来,数学家把这个规则推广到:
分数的运算
负数的运算
无理数的运算
代数式的运算
方程的运算
函数的运算……
所有这些运算,都是建立在"先乘除后加减"这个基础规则之上的。
因此,咱得让孩子理解——孩子的问题往往很有深度,讲明白理解透了,就是数学思维提升的时刻。
数学思维并不高大上,一点一滴,都在平时。

 备案号:
备案号: